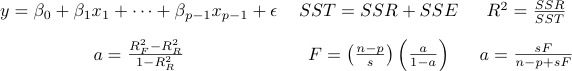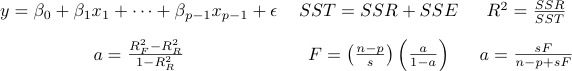Assignment Six: Quiz
on Friday March 1st in tutorial
This assignment is on regression with normal error terms. It is based on Lecture slide sets 9 and 10, and material in Chapter 5 of the online text. The following formulas will be provided with the quiz (and the final exam), whether they are needed or not:
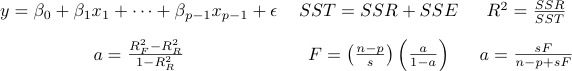
- Children were randomly assigned to one of three toothpaste formulas, and instructed to brush their teeth. The length of time they brushed was recorded. Age in months was a covariate.
- Write E(y|x) for a regression model with parallel regression lines. Denote age by x, and put it last. Use cell means coding. That's the set-up with indicator dummy variables and no intercept.
- Make a table showing how your dummy variables are set up. There should be one row for each toothpaste, and a column for each dummy variable. Add a wider column on the right, in which you show E(y|x) for each toothpaste. Note that the symbols for your dummy variables will not appear in this column.
- For each of the following questions, give the null hypothesis in terms of the β parameters of your regression model. Remember that we are not doing one-tailed tests in this class.
- Controlling for age, does average brushing time differ for the three toothpaste formulas?
- Give the null hypotheses you would test for all pairwise comparisons.
- Controlling for age, is average brushing time different for toothpaste formula One, versus the mean of Two and Three?
- Now consider the problem of incorporating non-parallel regression lines (interactions) in a model with cell means coding. This question was changed substantially on Tuesday Feb. 20th.
- Your first thought might be to add product terms of all the dummy variables with the covariate to your model. For the diet data, that would be three product terms. What is the sum of the three product terms? Is this a problem?
- So, one of the terms in the regression model is redundant. It could be one of the product terms, or it could be x.
Write E(y|x) for a regression model with all three dummy variables and all three product terms, but no x. It's strange, but observe how nicely this works out.
- The rule about these dummy variable schemes is that if you do it right, they are all equivalent. Therefore, this model and a model with an intercept should have the same number of parameters. Do they?
- Make a table showing how your dummy variables are set up. There should be one row for each toothpaste, and a column for each dummy variable. Add a wider column on the right, in which you show E(y|x) for each toothpaste. The symbols for your dummy variables will not appear in this column. Be able to read off the slope and intercept for each toothpaste.
- For each of the following questions, give the null hypothesis in terms of the β parameters of your regression model. Remember that we are not doing one-tailed tests in this class.
- Are the three slopes equal?
- Is there an interaction between age and toothpaste type?
- Do the differences in average brushing time between the three toothpastes depend on the child's age?
- Do age differences in brushing time depend on the type of toothpaste?
- Is the increase in average brushing time with age the same for toothpaste types Two and Three?
- In the Diet Data from Assignment 4, we have
- Person: Identification code
- gender: F or M
- Age: In years
- Height: In cm.
- pre_weight: Weight in kg. before starting the diet.
- Diet: 1, 2, or 3, randomly assigned
- weight6weeks: Weight in kg. after 6 weeks on the diet
When you have a "before" and an "after" measure like this, the following question often arises. Should you compute change, or should you control for the before measurement using regression? Here, we'll control for it, and the response variable will be weight after 6 weeks on the diet.
For this problem, please include an intercept in all your regression models. We will get to no-intercept models with SAS later.
- Just for comparison, let's use proc reg check whether diet has an effect on weight after six months, not controlling for any other variables.
- Write E(y|x) in Greek letters. You do not have to say how your dummy variables are defined. You will do that in the next part.
- Make a table with one row for each diet. Make columns for the dummy variables, using your SAS variable names to label the columns. Add a wider column on the right, showing E(y|x) for each diet. The symbols for your dummy variables should must not appear in the last column, because they are either zero or one.
- To test whether diet had any effect, what is the null hypothesis? Give your answer in symbols. Why is it okay to use the word "effect?"
- Fit the model, meaning estimate the parameters. Ignoring all other potential predictors, what proportion of the variation in weight after 6 months is explained by diet? The answer is a number from your printout.
- For the test of whether diet had an effect on weight after 6 months, fill in the table below.
| Test Statistic (F or t) |
p-value |
Reject H0 at 0.05 level? |
Statistically significant? |
|
|
|
|
- In plain, non-statistical language, what do you conclude from this test?
- Check your F statistic using proc glm.
- Weight before and after the diet should be correlated. What is the (Pearson) correlation? What proportion of the variation in weight after 6 weeks is explained by weight before the diet? You could use either proc iml or a calculator for this one.
- Now consider a model in which the explanatory variables are diet, and weight before starting the diet. Other variables are ignored for now. This is very different from controlling for them.
- Write E(y|x) in Greek letters. Denote weight before starting by x1.
- Make a table with one row for each diet. Make columns for the dummy variables, using your SAS variable names to label the columns. Add a wider column on the right, showing E(y|x) for each diet. The symbols for your dummy variables should must not appear in the last column, because they are either zero or one.
- Using proc reg, fit the model. Include the simple option, because you will need one of the means later. You should also request two custom tests: Diet controlling for weight before, and the pairwise comparison of diets that is missing from the default proc reg output.
- For the test of whether diet had an effect controlling for weight before the experiment, fill in the table below.
| Test Statistic (F or t) |
p-value |
Reject H0 at 0.05 level? |
Statistically significant? |
|
|
|
|
- Using proc iml, produce Bonferroni-corrected p-values for all three pairwise comparisons of diets controlling for weight before. Your Bonferroni family has three tests.
- You want to draw directional conclusions, and you could based on your table. However, let's produce something nicer. For each diet calculate a y-hat value with pre_weight set to its overall sample mean value. So, you are getting a predicted (estimated mean) weight for a participant whose weight before the experiment was average. I would call these "corrected means." Use proc iml.
- In plain, non-statistical language, what do you conclude about the diets? Don't use the word "controlling." Choose a less technical term.
- Now replicate the analysis with proc glm, including Bonferroni-corrected comparisons of the diets controlling for weight before the experiment. How do the lsmeans from proc glm compare to your corrected means?
- In Question 3b, you obtained the proportion of variation in weight after 6 weeks explained by weight before the diet. In the formulas given at the beginning of this assignment, you have two formulas for calculating the proportion of remaining variation in weight that is explained by Diet, after controlling for weigh before the study. Using proc iml, calculate this number two ways.
- The data file has some variables you have not used yet. Check whether they are related to weight after 6 weeks, controlling for weight before the study and Diet. Test them simultaneously. What do you conclude?
- Up until this point, regression lines for the three diets have been parallel. This is an assumption. Test it, using the model with just Diet and weight before the experiment.
Bring your log and results files to the quiz. Do not write anything
on the printouts in advance except your name and student number. You may be
asked to hand them in. The log and list files must
be generated by the same SAS program. There
must be no errors or warnings in your log files. Bring a calculator to the quiz.
You may not put conclusions in in comment statements, or otherwise cause them to appear on your printouts. If you do this, it's an unauthorized aid -- an academic offence.

This assignment is licensed under a Creative Commons Attribution-ShareAlike 3.0 (or later) Unported License. Use and share it freely.