Assignment 11

STA441 Assignment 11

A few extra Questions for the final exam: No quiz

Questions 1 and 2 are about the multivariate approach to repeated measures. My answers are HERE.

A random sample of male and female university students is weighed midway through year 1, 2, 3 and 4.
1. What are the cases in this study?
2. How many numbers (observations) do you have for each student?
3. This is a factorial experiment. What are the factors?
4. Classify each factor as between-cases or within-cases.
5. In the multivariate approach to within-cases analysis, you set up effect coding dummy variables for the between-cases factors (if any), and calculate response variables that are linear combinations of the variables that are recorded for each case. You can then obtain tests for all the main effects and interactions by testing null hypotheses about the β values in the regression model. Sometimes the model has more than one response variable (linear combination). In this case it really is multivariate, and the second subscript on the βs (see formula sheet) refers to the response variable.
  Denote the four weights for student i by y_i1, y_i2, y_i3, y_i4. The response variables will be linear combinations of these values. First consider the main effect for gender of student.
  1. Give a formula (or formulas) for the linear combination (or combinations) that you would use as the response variable (or variables).
  2. Write the regression model -- just the expected value(s).
  3. In terms of the β values from your model, what is the null hypothesis corresponding to no main effect of gender?
6. A single model applies to Year and Gender by Year.
  1. Give a formula (or formulas) for the linear combination (or combinations) that you would use as the response variable (or variables).
  2. Write the regression model -- just the expected value(s).
  3. In terms of β values from your model, what is the null hypothesis for testing the main effect of Year?
  4. In terms of β values from your model, what is the null hypothesis for testing the Gender by Year interaction?

In an experiment on anxiety medications, volunteer patients took a pill in the morning every day and in the evening they rated how anxious they had felt on average during that day. What was in the pill was unknown to the patient, and came in a different random order for every patient. The pill contained Drug A (Yes or No) and Drug B (Yes or No), in all four combinations. The four numbers for each patient are actually average ratings over 10 cycles, so the experiment took 40 days. The four numbers for each patient are

y₁₁: Average rating in the No, No condition. E(y₁₁)=μ₁₁
y₁₂: Average rating in the No, Yes condition. E(y₁₂)=μ₁₂
y₂₁: Average rating in the Yes, No condition. E(y₂₁)=μ₂₁
y₂₂: Average rating in the Yes, Yes condition. E(y₂₂)=μ₂₂

What are the cases in this study?
This is a factorial experiment. What are the factors? (Let's say that case is not a factor.)
Classify each factor as between-cases or within-cases.
Make a 2 by 2 table and write expected values in the cells.
You can test the main effects and interactions in this study with one-sample t-tests, testing whether the means of certain linear combinations of the y_ij variables equal zero. Give the linear combination you would use to test for each of the following. In each case, the answer is a formula, a function of the y_ij.
1. Main effect for Drug A .
2. Main effect for Drug B .
3. Drug A by Drug B interaction.

Psychoactive drugs can have very different effects depending on the age of the person taking them. So consider independent samples of patients aged 5-12, 13-18, 19-29, 30-64 and 65+.

Write a regression model with an intercept, in which the expected value of the response variable ℓ depends on age group. You don't have to specify how your dummy variables are defined. You will do that in the next part.
Make a table with 5 rows, showing how your dummy variables for age group are defined with effect coding. That's the set-up with 0, 1, -1. Add another column for the expected value of the response variable.
Why is your dummy variable coding scheme a good choice for testing whether the average expected value of the linear combination (averaging over age) is equal to zero?
We now have a 3-factor design, with one between-cases factor and 2 within-cases factors. What is the between-cases factor?

For each of the effects in your 3-way design, give the linear combination of y_ij, you would use as the response variable, and the null hypothesis you would test in terms of β values from your regression model.

Effect	Linear combination	Null hypothesis
Drug A
Drug B
Age
A × B
A × Age
B × Age
A × B × Age

For this question, the analyses will be based on fixed effects models using proc mixed. The model is linear regression, possibly with dummy variables:

Y_i = β₀ + β₁x_i1 + β₂x_i2 + ... + β_px_ip + ε_i,

where the error terms ε_i are normally distributed with expected value zero. Error terms for the same case have a covariance matrix Σ. The matrix Σ could be have all σ² values on the main diagonal and zeros on the off-diagonals. In this case we have ordinary regression with independent errors.

Quite a few other structures are available for Σ, including the following:

Unknown (type=un) Variance Components (type=vc) Compound Symmetry (type=cs) Autoregressive (type=ar(1))

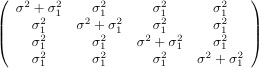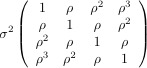These formulas will be provided with the last quiz (in 2016), and they will be on the formula sheet for the final exam. For any set of proc mixed output you generate, you should be able to

Give p, the number of explanatory variables in the regression model.
Give the dimension (number of rows and columns) in Σ.
Give the total number of parameters in the model you fit. That's the number of β values plus the number of unique elements in Σ.
Locate any parameter estimates on your printout.
For every test (and there may quite a few) be able to state the null hypothesis in terms of the symbols of your model.

In a test of how well people remember instructional materials, subjects of various educational levels were presented with training materials that were either in Black & White or in Colour. Their ability to recall the material was tested with both Cartoon and Realistic testing materials at two points in time -- immediately after training, and several weeks later. Scores on an IQ test (the Otis Mental Ability Test) were available for all subjects. The variables are

Subject identification number
Colour of training materials: 0 = Black & White, 1 = Colour
Education: 0 = Pre-professional, 1 = Professional, 2 = Student.
Location: 1 = Hospital A, 2 = Hospital B, 3 = Hospital C, 4 = Penn State University.
Otis Test of Mental Ability (IQ)
Recall at Time One, Cartoon testing materials
Recall at Time One, Realistic testing materials
Recall at Time Two, Cartoon testing materials
Recall at Time Two, Realistic testing materials

The data are available in the file cartoon.data.txt. This is a Minitab data set.

We will limit the analysis to students, who are all from Penn State University. I used an if statement, but I had to put if before output.This leaves us with a three-factor analysis of covariance.
1. What is the covariate?
2. What are the factors?
3. Label each factor as within-cases or between-cases.
Write the full regression model, with products of dummy variables for all possible interactions. I get 9 βs.
Give the dimension (number of rows and columns) in Σ.
Let's not assume anything about the structure of the covariance matrix. How many unique elements are there in Σ?
Carry out the analysis using proc mixed. Just so you can see if we are on the same page, my -2 Restricted Log Likelihood was 878.6.
1. For each F-test, be able to state the null hypothesis in Greek letters.
2. Locate the estimate of each element of Σ on your printout. Don't bother with the β-hats.
3. For each significant F-test, be able to state the conclusion in plain, non-statistical language. This will require some lsmeans.
4. What is the null hypothesis for the "Null Model Likelihood Ratio Test?" Why does it have 9 degrees of freedom?

Describe an original study that would call for a multivariate regression in which you control for an unordered categorical explanatory variable and then test the relationship of two quantitative explanatory variables to two response variables simultaneously. Be sure to specify which are the explanatory variables and which are the response variables, and which of the variables you are controlling for. If a variable is to be represented by dummy variables you should mention this and say how many dummy variables, but you don't need to say exactly how they are defined or go into further detail. Don't bother to say anything about test statistics or pvalues. The study must be original or you will get no marks.
Design an original study that would use a three-way multivariate analysis of covariance.
Design an original study that would use a logistic regression with one quantitative explanatory variable and dummy variables for a categorical explanatory variable with 3 categories.
Is it possible to have a study with repeated measures and a categorical response variable? If it is possible, make up an original example. If it is impossible, explain why.
Make up an original example of a study that is multivariate, and both response variables are categorical.
Invent and briefly describe (in a few sentences at most) original studies with the following characteristics. Do not use any examples from lecture or the class notes. If the requested example is impossible, say so and explain why it is impossible. The word original is important. If you give an example that is overly similar to one from lecture or the class notes, your answer will receive a zero. If two people give exactly the same example, they will both get a zero for the question.
1. A categorical explanatory variable and a continuous response variable.
2. A continuous explanatory variable and a continuous response variable.
3. A nominal scale explanatory variable and an ordinal scale response variable.
4. An explanatory variable that is both quantitative and nominal scale, and a response variable that is continuous.
5. Two categorical explanatory variables and two categorical response variables.
6. A single categorical explanatory variable and two quantitative response variables

Unknown (`type=un`)		Variance Components (`type=vc`)		Compound Symmetry (`type=cs`)		Autoregressive (`type=ar(1)`)