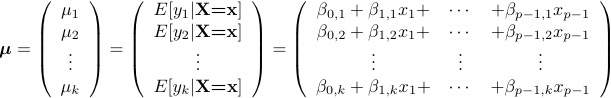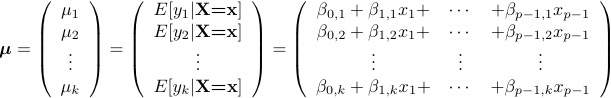STA441 Assignment 9

Quiz in Tutorial on Monday March 16th

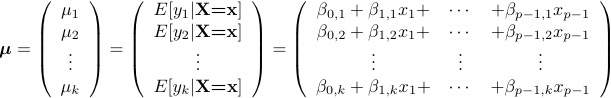
1. A random sample of male and female university students is weighed midway through year 1, 2, 3 and 4.
   1. What are the cases in this study?
   2. How many numbers (observations) do you have for each student?
   3. This is a factorial experiment. What are the factors? (Let's say that case is not a factor.)
   4. Classify each factor as between-cases or within-cases.
   5. Make a 2 by 4 table. Draw an oval or ovals on the table, indicating the crossing or nesting of cases within experimental conditions. See the lecture slides for some examples.
   6. In the "multivariate" approach to within-cases analysis, you set up effect coding dummy variables for the between-cases factors (if any), and calculate response variables that are linear combinations of the variables that are recorded for each case. You can then obtain tests for all the main effects and interactions by testing null hypotheses about the β values in the regression model. Sometimes the model has more than one response variable (linear combination). In this case it really is multivariate, and the second subscript on the βs refers to the response variable.

      Denote the four weights for student i by y_i1, y_i2, y_i3, y_i4. The response variables will be linear combinations of these values. First consider the main effect for gender of student.

      1. Give a formula (or formulas) for the linear combination (or combinations) that you would use as the response variable (or variables).
      2. Write the regression model -- just the expected value(s).
      3. In terms of the β values from your model, what is the null hypothesis corresponding to no main effect of gender?
   7. A single model applies to Year and Gender by Year.
      1. Give a formula (or formulas) for the linear combination (or combinations) that you would use as the response variable (or variables).
      2. Write the regression model -- just the expected value(s).
      3. In terms of β values from your model, what is the null hypothesis for testing the main effect of Year?
      4. In terms of β values from your model, what is the null hypothesis for testing the Gender by Year interaction?
   
   
2. In an experiment on anxiety medications, volunteer patients took a pill in the morning every day and in the evening they rated how anxious they had felt on average during that day. What was in the pill was unknown to the patient, and came in a different random order for every patient. The pill contained Drug A (Yes or No) and Drug B (Yes or No), in all four combinations. The four numbers for each patient are actually average ratings over 10 cycles, so the experiment took 40 days. The four numbers for each patient are
   
   
   • y₁₁: Average rating in the No, No condition. E(y₁₁)=μ₁₁
   • y₁₂: Average rating in the No, Yes condition. E(y₁₂)=μ₁₂
   • y₂₁: Average rating in the Yes, No condition. E(y₂₁)=μ₂₁
   • y₂₂: Average rating in the Yes, Yes condition. E(y₂₂)=μ₂₂
   
   
   1. What are the cases in this study?
   2. This is a factorial experiment. What are the factors? (Let's say that case is not a factor.)
   3. Classify each factor as between-cases or within-cases.
   4. Make a 2 by 2 table and write expected values in the cells.
   5. Make an oval or ovals on the table, indicating the crossing or nesting of cases within experimental conditions. See the lecture slides for some examples.
   6. You can test the main effects and interactions in this study with one-sample t-tests, testing whether the means of certain linear combinations of the y_ij variables equal zero. Give the linear combination you would use to test for each of the following. In each case, the answer is a formula, a function of the y_ij.
      1. Main effect for Drug A .
      2. Main effect for Drug B .
      3. Drug A by Drug B interaction.
   7. Psychoactive drugs can have very different effects depending on the age of the person taking them. So consider independent samples of patients aged 5-12, 13-18, 19-29, 30-64 and 65+.
      1. Write a regression model in which the expected value of the response variable depends on age group. You don't have to specify how your dummy variables are defined. You will do that in the next part.
      2. Make a table with 5 rows, showing how your dummy variables for age group are defined. Add another column for the expected value of the response variable.
      3. Why is your dummy variable coding scheme a good choice for testing whether the average expected value of some linear combination is equal to zero?
      4. We now have a 3-factor design, with one between-cases factor and 2 within-cases factors. What is the between-cases factor?
      5. For each of the effects in your 3-way design, give the linear combination of y_ij, you would use as the response variable, and the null hypothesis you would test in terms of β values from your regression model.
         
         

         Effect	Linear combination	Null hypothesis
         Drug A
         Drug B
         Age
         A × B
         A × Age
         B × Age
         A × B × Age

   
   
3. In an experiment on perception and attention, left-handed and right-handed subjects push a key when they hear their names over background noise. They are wearing stereo headphones. The signal comes in the left ear, the right ear, or both. There are 50 trials in each condition, presented in a different random order for each subject. The response variable is median reaction time in milliseconds. Each subject contributes 3 medians. The data are available in HandEar.data.txt.
   1. How many factors are there in this study? Classify each one as between cases or within cases. Let's say that case is not a factor.
   2. Make a 2 by 3 table. Draw an oval or ovals on the table, indicating the crossing or nesting of cases within experimental conditions.
   3. Use proc tabulate to produce a two-way table of treatment means.
   4. Use proc glm to make an interaction plot. Of course you should not believe the significance tests, because they are based on a purely between-cases model.
   5. Use proc mixed to do the following. Because a piece of random noise from each subject seems reasonable, choose the compound symmetry covariance structure.
      1. Test for the main effects and the interaction.
      2. Only one of the three standard tests was significant at the 0.05 level. Follow it up the simplest and most natural way, with Bonferroni-corrected multiple comparisons. In simple, non-statistical language, what do you conclude?
   6. For comparison (and for practice), carry out the same analysis using the multivariate approach to repeated measures. I had to read the data file again, a different way. You can read multiple lines per case with no problem. Read every number, and give every variable a name, even if they are repeats.
      1. Use proc means to get the same means you obtained with proc tabulate above. Once you've done this, you know you are reading the data correctly.
      2. Now do the tests for main effects and interactions using proc glm with a repeated statement. Do the multivariate tests lead to different conclusions than the ones suggested by proc mixed? You can verify that your code is correct when the "univariate" tests produced by proc glm correspond to the tests you got from proc mixed with the type=cs option.
      3. Finally, use proc reg to reproduce just the test of main effect for presentation (or ear: left vs. right vs. both). That is, you're reproducing the multivariate test of main effect you got from proc glm.
      4. If you've come this far, you also see how you would do the multiple comparisons of marginal means. You don't have to do it, though. The Bonferroni-corrected p-values are a bit different from the ones you got from proc mixed, though they lead to the same conclusions. Yes, this last part of the last question asks you to do nothing at all.

Please bring your log file and results file to the quiz. As usual, answers to the questions are not to be handed in. They are just practice for the quiz. Please do not write anything on your printouts except your name and student number. It is okay to highlight the results files, but do not write interpretations on your results files, or cause them to appear in any way (including comment statements) on your log files.