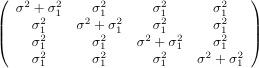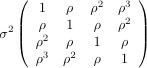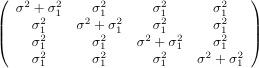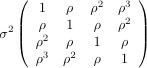STA441 Assignment 10

Quiz in Tutorial on Tuesday March 27th

Unknown		Compound symmetry		Autoregressive

This assignment uses 2 different data sets, so please bring 2 separate sets of output, the log file and the results file for each data set. You may not hand all of them in.

1. In a test of how well people remember instructional materials, subjects of various educational levels were presented with training materials that were either in Black & White or in Colour. Their ability to recall the material was tested with both Cartoon and Realistic testing materials at two points in time -- immediately after training, and several weeks later. Scores on an IQ test (the Otis Mental Ability Test) were available for all subjects. The variables are
   • Subject identification number
   • Colour of training materials: 0 = Black & White, 1 = Colour
   • Education: 0 = Pre-professional, 1 = Professional, 2 = Student.
   • Location: 1 = Hospital A, 2 = Hospital B, 3 = Hospital C, 4 = Penn State University.
   • Otis Test of Mental Ability (IQ)
   • Recall at Time One, Cartoon testing materials
   • Recall at Time One, Realistic testing materials
   • Recall at Time Two, Cartoon testing materials
   • Recall at Time Two, Realistic testing materials

   The data are available in the file cartoon.data.txt. This is a Minitab data set.

   We will teat this as a four-factor analysis of variance, ignoring the other variables. Please use the "multivariate" approach to repeated measures. That is, you will be using proc reg or proc glm, not proc mixed.

   The factors are Colour of training materials, Eduction, Time (One versus Two), and Testing materials (Cartoon versus realistic). Take a look at the raw data. See all the missing values? This does not make us feel comfortable, but we will proceed anyway and analyze the cases with no missing data. It's helpful to completely exclude cases with any missing data. A search on SAS subset if will show you an easy way to do this.

   1. Classify the factors as within-cases or between-cases.
   2. Carry out the analysis, obtaining tests of all the main effects and interactions. How many tests are you doing? Be ready with all the F statistics and p-values.Remember, if you give proc reg a list of response variables, you get univariate output for each response variable. The results of test statements come in a particularly handy format. These results are a relief. They will be easy to talk about.
   3. Carry out Bonferroni-corrected pairwise comparisons of the marginal means for education. This is a family of just three tests. In plain, non-statistical language, what do you conclude? I did this by running proc glm on my sum variable and using lsmeans.
   4. Sticking strictly to the 0.05 significance level, did you get any significant interactions? Answer Yes or No. If Yes, which ones were significant?
   5. For each of the significant main effects, describe the resullts in plain, non-statistical language. You don't have to say "averaging across other factors" or anything. Just say what happened.
   Bring your log file and results file to the quiz.
   
   
2. The file BeatTheBlues.data.txt was originally an R data set. It contains data from a longitudinal clinical trial of an interactive, multimedia program known as "Beat the Blues" designed to deliver cognitive behavioural therapy to depressed patients via a computer terminal. Basically, cognitive behavioural therapy is a set of techniques for getting people to think about things in a more positive, constructive way.

   Patients with depression recruited in primary care were randomised to either the Beating the Blues program, or to "Treatment as Usual" (TAU). The variables are

   • id: Patient identification code
   • drug: Did the patient take anti-depressant drugs (No or Yes).
   • length: The length of the current episode of depression, a factor with values <6m (less than six months) and >6m (more than six months).
   • treatment: Treatment group, a factor with levels TAU (treatment as usual) and BtheB (Beat the Blues)
   • bdi_pre: Beck Depression Inventory score before treatment.
   • bdi_2m: Beck Depression Inventory score after two months.
   • bdi_4m: Beck Depression Inventory score after four months.
   • bdi_6m: Beck Depression Inventory score after six months.
   • bdi_8m: Beck Depression Inventory score after eight months
   .
   1. This is a very rich data set, and I did a lot of exploration. You can also do whatever you want of course, but at least please do the following.
      1. Look at the raw data. There are a lot of missing values. Do you see a pattern?
      2. Read the data and calculate the following new variables: A zero-one indicator dummy variable for whether the patient was taking anti-depressant medication, a zero-one indicator dummy variable for whether the patient quit before the study was finished, and change scores from the baseline depression measurement, representing improvement.
      3. Obtain frequency distributions of all the categorical variables and use proc means to get basic desctiptive statistics for the Beck inventory scores and improvement scores. I recommend the maxdec=3 option. How many people participated in the study?
      4. Looking at those mean change scores, I wonder what happened just for those patients in the "Treatment as usual" condition who were not on drugs. My expectation as I type this before doing the analysis is that they showed significant improvement at each time period. Is this correct? Just do 4 matched t-tests. Don't forget to produce the actual means and sample sizes.
      5. Make a correlation matrix of all the Beck depression scale scores, and also include your indicator variables for drug and quitting. The correlation of a quantitative variable with an indicator is meaningful; it's called a point-biserial correlation. You can believe the p-value. Look at the results and be ready to state the conclusions.
      6. Given that patients were randomly assigned, should there be a relationship between treatment and whether the patient is taking drugs? What do the data say? State your conclusion in plain, non-statistical language.
      7. It's possible that patients who are more depressed to start with are more likely to quit and leave the study. Or maybe they are less likely to quit, because they need help more. I am thinking of a simple model with pre-test as the explanatory variable and quitting Yes-No as the response variable. Do it. What do you conclude? Are these results consistent with what you saw in the correlation matrix?
      8. Now do simple chi-squared tests of independence to determine whether being on medication, length of depression episode or experimental treatment is related to quitting the study. Suppose one of the researchers running the study concludes that quitting appears to be pretty much at random with respect to the other variables in the study. Do you agree, or do you disagree? Why?
      
      
   2. Since very few patients are missing at the two-month follow-up, it's natural to use the Beck score at 2 months as the sole response variable.
      1. Probably the simplest analysis you can do is to just compare mean depression score at two months for the treatment group and the control group. Use proc glm. Don't forget the means statement. State your conclusion in plain, non-statistical language.
      2. For a more refined analysis, do the same thing using change (improvement) from the baseline measurement. In plain, non-statistical language, what do you conclude?
      3. Instead of using change as the response variable, go back to depression at 2 months as the response variable, and adjust for the baseline measure by treating it as a covariate. This time you will need to use lsmeans rather than means. What do you conclude now?
      4. Because of the relationship between being on medication and experimental treatment, we decide not to ignore medication. Treat it as a covariate, without any interaction between medication and treatment. That is, fit a model with depression at 2 months as the response variable. The explanatory variables are being on medication, baseline depression measurement and experimental treatment. What do you conclude now?
      5. Which of these analyses is the right one? Think about it for a moment. Click here for the answer.
      
      
   3. Using the multivariate approach to repeated measures, carry out a treatment by time factorial analysis of variance, using improvement compared to baseline as the response variable. What do you conclude from the tests for main effects and interactions? There are the only tests I'm going to look at. One of them is significant. Without any formal follow-up tests, what seems to be going on?
   4. Now we're going to try the covariance structure approach. There are many ways to do it, but to give the Beat the Blues treatment the best possible chance, we're going to adjust for baseline measurement by treating it as a covariate. Also, because of what we found from the correlation matrix, we're not going to control for whether they were on medication. This also may be tilting the analysis in favour of finding an effect of treatment. So we have a treatment by time design, with baseline depression measurement as a covariate. First, try the analysis with an unknown covariance structure.
      1. For the ``Null Model Likelihood Ratio Test," what is the null hypothesis? Give the answer in Greek letters.
      2. Does the Null Model Likelihood Ratio Test support the need use of a within-cases analysis? Answer Yes or No. Briefly state why.
      3. In the Type 3 Tests of Fixed Effects, naturally the covariate was significantly related to the response variable. One other effect was significant. What was it?
      4. Follow up with a Bonferroni-corrected multiple comparison. Hint: I needed two separate lsmeans statements. The results are a bit clumsy to describe in detail, but in broad general terms, what have you found? Use plain, non-statistical language.
      5. We are not quite prepared to give up on experimental treatment. Let's test the null hypothesis that controlling for pre-test, there is no mean difference between treatment and control at any time period. This is a null hypothesis of conditional independence. If it is rejected (and only then), follow up with Bonferroni-corrected tests at each time period. How many follow-up tests are in this Bonferroni family? What do you conclude?
      
      
   5. The ar(1) covariance structure is an attractive choice for this problem, since the data are collected at equally spaced points in time. Now, the ``Null Model Likelihood Ratio Test" statistic equals the -2 log likelihood for a diagonal Σ with equal diagonal elements, minus the -2 log likelihood for the unstructured covariance matrix. This means that since the ar(1) is a special restricted case of the un structure, one can test the null hypothesis of ar(1) (restricted model) against the alternative of un (unrestricted model) by simply subtracting the chi-squared statistics and subtracting the degrees of freedom. If the null hypothesis is rejected, you have a case against ar(1), so don't use it. If you don't reject H₀, we have the green light to use the ar(1) model. So go ahead and fit the treatment by time design with baseline depression measurement as a covariate again, but this time use the first-order autoregressive structure.
      1. Carry out the likelihod ratio test just described. It doesn't matter whether you calculate the test statistic with a calculator or proc iml, but you will have to use proc iml to obtain the critical value. Look up the quantile function online. What do you conclude? Is it okay to use ar(1)?
      2. If it's okay, take a look at the F-tests. Do your conclusions change? If so, what do you conclude now?
      
      
   
   Bring your log file and results file to the quiz.
   

Please bring both log files and both results files to the quiz. As usual, answers to the questions are not to be handed in. They are just practice for the quiz.