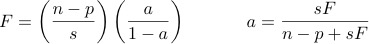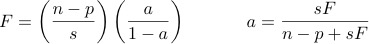Assignment Five: Quiz on Thursday Feb. 11th in tutorial

he following formulas will be provided with the quiz (and the final exam), whether they are needed or not:

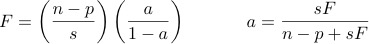
Telephone sales representatives use computer software to help them locate potential customers, answer questions, take credit card information and place orders. Twelve sales representatives were randomly assigned to each of three new software packages the company was thinking of purchasing. The data for each sales representative include the software package (1, 2 or 3), sales last quarter with the old software, and sales this quarter with one of the new software packages. Sales are in number of units sold. The data are in the file sales.data.txt. We will treat sales this quarter as the response variable and sales last quarter as a covariate.

1. First, ignoring which new software package the sales representative employed, are sales better on average this quarter than last quarter? Do the simplest, most basic test you can. Give the numerical value of the test statistic (t, F or chi-square), the p-value, and state your conclusions in plain, non-statistical language.
2. Now write E[Y|X] for a regression model in which the slope of the regression line relating sales this quarter to sales last quarter might depend on which software was used. This is pure paper-and-pencil, not SAS.
3. Make a table showing how you defined the dummy variables for software package. Make number 3 the reference category. Add a column showing E[Y|X] for each software. This is pure paper-and-pencil, not SAS.
4. Using SAS, fit your model to the sales data. Using a calculator or proc iml and the numbers from proc reg simple, give
   1. The estimated slope and intercept of the regression line relating sales this quarter to sales last quarter, for sales representatives using software package 1.
   2. The estimated slope and intercept of the regression line relating sales this quarter to sales last quarter, for sales representatives using software package 2.
   3. The estimated slope and intercept of the regression line relating sales this quarter to sales last quarter, for sales representatives using software package 3.
   4. Estimated sales this quarter for a representative with average (sample mean) sales last quarter, using software package 2.
5. Now, test the null hypothesis of equal regressions. That is, the null hypothesis is that the three regression lines are right on top of each other, and there is no difference in expected sales as a function of software used, for any value of sales last quarter.
   1. In terms of the symbols of your regression model, what is the null hypothesis?
   2. Give the test statistic (a number from your printout) and the p-value.
   3. Agree or Disagree: There is not sufficient evidence to conclude that expected sales are different using the 3 software packages, for any value of sales last quarter.
6. Now, test whether an assumption of parallel regression lines is justified.
   1. In terms of the symbols of your regression model, what is the null hypothesis?
   2. Give the test statistic (a number from your printout) and the p-value.
   3. Consider (in your mind; don't fit it) a reduced model with equal slopes. This model explains a certain amount of the variation in sales this quarter. What proportion of the remaining variation is explained when we add those product terms to the model, allowing the slopes to be unequal? The answer is a number you could calculate from your output. My answer is 0.4071146. If you get this number, we must be doing lots of other things the same way too.
   4. Agree or Disagree: There seems to be an interaction between software package used and sales last quarter.
7. By default, proc glm produces a lovely plot of the three regression lines over the range of the data. Fit the model using proc glm, including interactions. Naturally, you will not use your product term variables; let SAS do it.
   1. See the pretty picture? Is it consistent with your answer to Question 4?
   2. Look at the F tests for the Type III sums of squares. In terms of the β values from your model of Question 2, what null hypothesis is each one testing?
8. We want to know whether there is a difference in mean sales this quarter for sales representatives with average (sample mean) sales last quarter. (I suppose that theoetically, there is a large sub-population of such sales representatives.)
   1. In terms of the symbols of your regression model, what is the null hypothesis
      1. If sales last quarter is centered?
      2. If sales last quarter is uncentered?
   2. Give the test statistic (a number from your printout) and the p-value. Do this the easiest, fastest way you can!
   3. Give mean sales for each software package, adjusted for sales last quarter. Yes, you are being asked for least squares means. Get them the easiest, fastest way you can.
   4. Agree or Disagree: For sales representatives with average sales last quarter, there is good evidence that software package 2 is better. Base your conclusion on the Bonferroni-corrected tests of pairwise differences between expected values.
9. Since there is evidence of unequal slopes, it is helpful to look at tests for pairwise differences between slopes. Carry these out with a Bonferroni correction, obtaining the Bonferroni-corrected p-values. What do you conclude? Here are some comments.
   • I got the p-values with proc reg, and then did the Bonferroni correction with a calculator.
   • Two of the p-values (before correction) were part of the default output.
   • You should be feeling pretty good about being able to do this. It's advanced, and at the same time it's very applied.
10. Give a prediction of sales for a sales representative who sold 70 units last quarter, and was using software package 1. Also, give a 95 percent prediction interval. There is an example of how to do this in the lecture slides.

Bring your log file and your results file to the quiz. Do not write anything on the printouts in advance except your name and student number. You may be asked to hand them in. The log and list files for each data set must be generated by the same SAS program or you may lose a lot of marks. There must be no errors or warnings in your log files. There must be no notes about invalid data. Bring a calculator to the quiz.