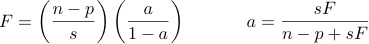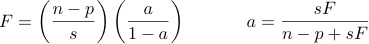Assignment Two: Quiz on Tuesday Jan. 23d in tutorial

This assignment is on regression with normal error terms. The conceptual part is mostly review, except for interactions. The assignment is based on Lecture slide sets 4 and 5, and material in Chapter 5 of the online text. The following formulas will be provided with the quiz (and the final exam), whether they are needed or not:

F <=< a

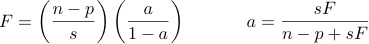
  1. High School History classes from across Ontario are randomly assigned to either a discovery-oriented or a memory-oriented curriculum in Canadian history. At the end of the year, the students are given a standardized test and the median score of each class is recorded. Please consider a regression model with these variables.:

    The full regression model is E[Y|X] = β0 + β1X1 + β2X2 + β3X3 + β4X4 + β5X5.

    For each question below, please give the null hypothesis in terms of β values. Also, give E[Y|X] for the reduced (restricted) model you would compare to the full model in order to answer the question. Don't re-number the variables.

    1. If you control for parents' education and income and for teacher's university background, does curriculum type affect test scores? (And why is it okay to use the word "affect?")
    2. Controlling for parents' education and income and for curriculum type, is teacher's university background (two variables) related to their students' test performance?
    3. Controlling for teacher's university background and for curriculum type, are parents' education and income (considered simultaneously) related to students' test performance?
    4. Controlling for curriculum type, teacher's university background and parents' education, is parents' income related to students' test performance?

  2. The U.S. Census Bureau divides the United States into small pieces called census tracts; lots of information is collected about each census tract. The census tracts are grouped into four geographic regions: Northeast, North Central, South and West. In one study, the cases were census tracts, the explanatory variables were Region and average income, and the response variable was crime rate, defined as the number of reported serious crimes in a census tract, divided by the number of people in the census tract.
    1. Write E(Y|x) for a regression model with parallel regression lines. You do not have to say how your dummy variables are defined. You will do that in the next part.
    2. Make a table showing how your dummy variables are set up. There should be one row for each region, and a column for each dummy variable. Add a wider column on the right, in which you show E(Y|x) for each region. Note that the symbols for your dummy variables will not appear in this column. There are examples of this format in the lecture slides and the text.
    3. For each of the following questions, give the null hypothesis in terms of the β parameters of your regression model. Remember that we are not doing one-tailed tests in this class.
      1. Controlling for income, does average crime rate differ by geographic region?
      2. Controlling for income, is average crime rate different in the Northeast and North Central regions?
      3. Controlling for income, is average crime rate different in the Northeast and Western regions?
      4. Controlling for income, is the crime rate in the South more than the average of the other three regions?
      5. Controlling for income, is the average crime rate in the Northeast and North Central regions different from the average of the South and West?
      6. Controlling for geographic region, is crime rate connected to income?
    4. Referring back to the previous set of questions, say why each of the following is a bad way to ask the question.
      1. Controlling for income, does geographic region affect the average crime rate?
      2. Allowing for geographic region, does average income have any effect on crime rate?
    5. Write E(Y|x) for a regression model in which the regression lines might not be parallel. For this new model, give the null hypothesis you would test in order to answer each question.
      1. Are the four regression lines parallel in the population?
      2. Is there an interaction between average income and geographic region?
      3. Does the relationship of average income to crime rate depend on geographic region?
      4. Do regional differences in average crime rate depend on the average income in the census tract?
      5. Is the slope of the line relating average income to expected crime rate different for the Northeast and North Central regions?
      6. Is the slope of the line relating average income to crime rate different for the Northeast and South regions?
      7. Is the slope of the line relating average income to crime rate different for the Northeast and West regions?
      8. Is the slope of the line relating average income to crime rate different for the North Central and South regions?
      9. Is the slope of the line relating average income to crime rate different for the North Central and West regions?
      10. Is the slope of the line relating average income to crime rate different for the South and West regions?

  3. Telephone sales representatives use computer software to help them locate potential customers, answer questions, take credit card information and place orders. Twelve sales representatives were randomly assigned to each of three new software packages the company was thinking of purchasing. The data for each sales representative include the software package (1, 2 or 3), sales last quarter with the old software, and sales this quarter with one of the new software packages. Sales are in number of units sold. The data are available in an Excel spreadsheet at

    http://www.utstat.toronto.edu/~brunner/data/legal/sales.data.xlsx

    1. Fit a model in which sales last quarter is ignored. This is very different from controlling for it. We want to know whether software package has any effect on sales. Why is it okay to use the word "effect?"
      1. Write E(y|x) in Greek letters.
      2. What proportion of the variation in sales this quarter is explained by software package? The answer is a number from your printout.
      3. What is the null hypothesis for testing whether software package has any effect on sales? Give the answer in terms of Greek letters from the regression model.
      4. Give the test statistic. The answer is a number from your printout.
      5. Give the p-value. The answer is a number from your printout. The p-value is not the same as the test statistic.
      6. Do you reject H0? Answer Yes or No.
      7. Are the results statistically significant? Answer Yes or No.
      8. Give the p-value (just the p-value, with no correction for multiple testing) for each pairwise comparison of software packages: That's 1 vs. 2, 1 vs. 3 and 2 vs. 3.
      9. In plain, non-statistical language, what do you conclude from this analysis?
    2. Now fit a model with software package and sales last quarter as the explanatory variables, and sales this quarter as the response variable. There are no interaction terms yet.
      1. Write E(y|x) in Greek letters. Make sure the variables are in the same order here and in your SAS program.
      2. What proportion of the remaining variation in sales this quarter is explained by software package once you allow for sales last quarter? The answer is a number that you calculate from the numbers on your printout. Bring a calculator to the quiz.
      3. What is the null hypothesis for testing whether software package has any effect on sales this quarter once you control for sales last quarter? Give the answer in terms of Greek letters from the regression model.
      4. Give the test statistic. The answer is a number from your printout.
      5. Give the p-value. The answer is a number from your printout.
      6. Do you reject H0? Answer Yes or No.
      7. Are the results statistically significant? Answer Yes or No.
      8. Give the p-value (just the p-value, with no correction for multiple testing) for each pairwise comparison of software packages controlling for sales last quarter: That's 1 vs. 2, 1 vs. 3 and 2 vs. 3.
      9. In plain, non-statistical language, what do you conclude from this analysis?
    3. Now fit a model in which the slopes as well as the intercepts might be different for the three software packages.
      1. Write E(y|x) in Greek letters. Make sure the variables are in the same order here and in your SAS program.
      2. What is the null hypothesis for testing whether the three slopes are equal? Give the answer in terms of Greek letters from the regression model.
      3. What is the null hypothesis for testing whether the effect of software program on sales this quarter depends on sales last quarter? Give the answer in terms of Greek letters from the regression model.
      4. What proportion of the remaining variation in sales this quarter is explained by unequal slopes once you allow for the other explanatory variables in the model? The answer is a number that you calculate from the numbers on your printout.
      5. Give the test statistic. The answer is a number from your printout.
      6. Give the p-value. The answer is a number from your printout.
      7. Do you reject H0? Answer Yes or No.
      8. Are the results statistically significant? Answer Yes or No.
      9. Estimate the slope of the line relating sales last quarter to sales this quarter, for software package 1. The answer may be directly on your printout, or it may be a number that you calculate from the numbers on your printout.
      10. Estimate the slope of the line relating sales last quarter to sales this quarter, for software package 2. The answer may be directly on your printout, or it may be a number that you calculate from the numbers on your printout.
      11. Estimate the slope of the line relating sales last quarter to sales this quarter, for software package 3. The answer may be directly on your printout, or it may be a number that you calculate from the numbers on your printout.
      12. Which of the three estimated slopes are significantly different from each other? You are summarizing the results of three tests.
    4. Clearly, the effect of software package depends on sales last quarter. Let's test the effect for a (hypothetical) average employee, someone whose sales last quarter were exactly at the sample mean. First, use proc iml to estimate expected performance this quarter for sales representatives with average performance last quarter. So we will get exactly the same answers, please use proc means to calculate the mean, and use all the decimal places in the printout. The result of the proc iml calculation is three numbers that will appear on your printout.
    5. State the null hypothesis: Use x-bar in your answer.
    6. Carry out the F-test. I was unable to do this with the test statment of proc reg. I had to center the covariate with proc standard and re-compute the product terms. Do you reject the null hypothesis? In plain, non-statistical language, what do you conclude?
  4. Just to guarantee that you know what's going on here, use proc iml again to to estimate expected performance this quarter for sales representatives with average performance last quarter. This time use the proc reg output for the centered data. Again your answer is a set of three numbers that appear on the printout. My answers agree with earlier results to two decimal places. Rounding error is inevitable if you are pulling numbers off printouts.

     

Bring your log and results files to the quiz. Do not write anything on the printouts in advance except your name and student number. You may be asked to hand them in. The log and list files must be generated by the same SAS program. There must be no errors or warnings in your log files. Bring a calculator to the quiz.

This assignment is licensed under a Creative Commons Attribution-ShareAlike 3.0 (or later) Unported License. Use and share it freely.